Phi zenbakia eta Jainkoaren begia
Pi zenbakiari buruz,
gutxi asko denok dakigu zerbait: π
simboloaz adierazten dela, bere balioa 3.14159… dela, zirkulu baten diametro eta perimetroaren arteko erlazioa dela (Perimetroa = pi * diametroa)…
Baina bada pi zenbakiak bezainbat propietate xelebre edo gehiago dituen beste
zenbaki bat ere. Phi zenbakiak hain zuzen (urrezko zenbakia bezala ere ezaguna).
Darren Aronofsky-ren pi filma ikusi baduzue agian ezagutuko duzue phi hau. Beno, edo agian hala eta guztiz ere ez, zeren eta filmean pi zenbakiaz baino gehiago phi zenbaki honetaz ari diren arren fita edo horrelakoren batez deitzen diote. (Nondik atera dute hori?).
Baina beno, zenbaki honen propietateeren bat ikusi aurretik eman ditzagun lehenik eta behin oinarrizko zenbait datu:
- Bere balioa 1.6180339... da eta atzetik, pi zenbakiak bezalaxe, infinitu dezimal ditu.
- Zenbaki honen berri greziarrek eta jada bazuten arren, Phi izena XX. mende hasieran eman zitzaion Fidias eskulturgile greziarraren omenez. Bere lanetan zenbaki hau aplikatu zuela uste baitzen.
- Jakina da greziarrek beraien bizitzan oreka aurkitzeko ahalegin handiak egin
zituztela, eta zenbaki hau kalkulatzeko erarik errazena ere ahalegin horiei zor diegu. Izan ere, L
luzerako lerro bat hartzen badugu eta modu “orekatu” batetan mozten saiatu,
beno, erditik moztea dugu L lerrotik (L/2) luzerako bi lerro txikiago lortuz,
baina bi parteen arteko oreka edo proportzio aproposena bere osotasunarekin konparatzean lortzen da, bi zati horiek L handiarekin izango duten erlazioa ikustean, eta zuzena bi zati desberdinetan mozten badugu (a eta b),
non, zatirik txikiena eta handienaren arteko erlazioa, zatirik handiena eta lerro
osoarern (a+b) artekoaren berdina den, orduan lortzen da phi zenbakia. Ikus dezagun:

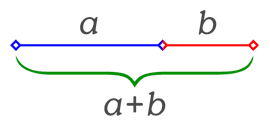 bada:
bada: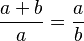 da, eta formula hau garatuz:
da, eta formula hau garatuz:eta bigarren mailako ekuazioa askatuz:
hau da: 
Eta (1+erro bost)/2 hori dugu Phi zenbakia, 1.618...
a = Phi x b
a zatia, b baino phi aldiz handiagoa denean moztu dugu lerroa era "orekatu" batetan.
Zenbaki hau, toki askotan agertzen da gure inguruan gu ez ohartu arren naturan: Loreen hostoak agertzen diren proportzioan, giza gorputzean (Le Corbusier arkitektoaren Modulor-aren oinarria da horregaitik), galaxien espiraletan...
Eta artean ere askotan erabili izan da, esan dugun bezala, batzuen ustez "oreka" sentsazioa berarekin zuelako. Greziako partenoiaren proportzioak zenbaki honetan oinarrituak daudela diote batzuk. Dirudienez, partenoiaren luzera eta altueraren arteko erlazioa 1.618... da. OINA = 1.618 x ALTUERA

Beste batzuen ustez egiptoko piramideetan ere ikusten da proportzio honen erabilera, garai hartan zenbaki hau ezagutzen zela erakusten duten frogarik ez dagoen arren (Pi zenbakia ordea bai, eta honen erdia, 3.14159-ren erdia, 1.57... da, Phi-ren antzekoa)
Errenazimenduan (greziar ideien errenazimenduan) ere zenbaki hau oso ezaguna izan zen eta Da Vinci-k bere Giocondan erabili zuela dioenik ere bada. Egia esan, irudia ikusiz hala dirudi:

baina hau baieztatzen duten datuak exkaxan dira.
Ikusi dugun bezala, aldeen arteko proportzio gixa zenbaki hau duten laukiluzeak badaude(la proporción áurea dutenez, rectángulos áureos deritzaie gazteleraz) hots, ALTUERA x 1.618... = OINA dutenak. Eta laukiluze honetan oinarritutako espiaral bat ere bada: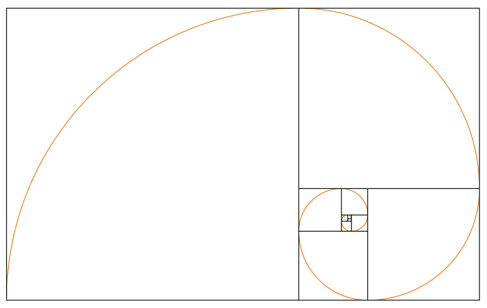
eta espiral hau da galaxietan maiz agertzen dena...
Bada baita ere laukiluze aureo honek duen propietate interesgarri bat. Izan ere, laukiluze honen barnean lauki bat marrazten badugu, berriz ere laukiluze aureo bat lortzen dugu. Goiko irudian ikusten da nola lauki bat marraztean (ezkerretako zatia) eskuinean laukiluze aureo bat geratzen zaigun (oraingoa "zutik" bertikalki), eta hau etengabe egiten badugu, azkenean espiralaren erpinera goaz. Puntu honi deitzen zaio JAINKOAREN BEGIA.
-----------------------------
Nik badut bestalde halako zaletasun xelebre xamar bat. Margolan famatuetan horrelako edo antzeko proportzio, estruktura eta arrasto "izkutuak" bilatzea gustatzen zait. Badakit margolanaren balioak ez datzala horretan soilik, baina gustoko dut. Horrela, Velázquezen Meninetara itzuli nitzen behin, eta oso gaizki ere ez zutela ezkontzen konturatu:

JAINKOAREN BEGIA VELÁZQUEZ-EN PALETA DA!!
eta interneten antzekorik dioen webgune bat bada! Hemen, laukiluze honetako izkutuko espiral aureoa kuadroan dagoen argi sarrerarekin konparatzen du...
Dalí-k ere bazioen Velázquez-en begirada cuasi-divinoa zela, Jainkoak sortua!
Kasualitate hutsa?
Agian bai, baina zein ondo pasa nuen hori egiten, eta ustez behinik behin aurkitzen! :-)
Wikipedia-n eta "La Proporció Áurea" liburuan oinarritua.



Iruzkinak
Itziar 2007-03-06 20:05 #1
matematika... <br /><br />egia esan ezkutuko gauza asko ditu matematikak. Oso interesgarria phi zenbakiaren kontu hori. <br /><br />post hau irakutzen ari nintzela Fibonacci-taz gogoratu naiz. Edo hobe esanda, aurreko urtean irakasle batek, ordura arte hainbeste aldiz entzun nuen Fibonacciren seriea nondik zetorren azaldu zigula. Ez al dakizue untxien istorioa? hasiera batean...egia izatetik urruti zebilela uste nuen. Baina internetek bestelakoa esan zidan. Begira <a href="http://www.formacion.pntic.mec.es/web_espiral/naturaleza/vegetal/fibonacci/fibonacci.htm">hemen</a>, oso ondo azalduta dator guri irakasleak kontatutakoa.<br />
borthuzai 2007-03-07 07:52 #2
<p>Jo! Oso artikulu interesgarria! Lehendik webgune horren berri izango banu ez nuke goiko liburua irakurri beharrik izango!:-)</p>
<p>Ez, benetan, “La proporción áurea” liburuan Fibonacci-ren historia hori eta beste mila xelebrekeria datoz, baina ni, azken batetan, zuk aipatzen duzun webgunean datorrenarekin geratu naiz: Phi-Fibonacci-Natura hirukoteaz eta adibideekin. Liburuaren laburpen gixa oso ondo dago artikulua.</p>
<p>(Liburuan bestalde, artea eta phi zenbakiaren arteko balizko erlazio ia guztiak (partenoian, piramideena, artela askoena…) farsa bat direla dio baita ere; gezurra dela laukiluze aureoak beste edozein laukiluzek baino “oreka” sentsazio handiagoa ematen duenik…)</p>
<p> </p>
<p><a href="http://www.rtve.es/tve/b/redes/semanal/prg364/entrevista.htm">Hemen</a>, <strong>La2</strong> eko <strong>Redes</strong> programarako Eduard Punset-ek liburuaren idazle den Mario Livio-ri egindako elkarrizketa topatuko duzue.</p>
Amuitz 2007-03-08 22:01 #3
Oso interesgarria. Zenbaki honek beste bi propietate betetzen ditu:<br /><ul><li>Unitate bat kentzen bazaio, bere alderantzizkoa ematen du: x-1=1/x</li>
<li>Unitate bat gehitzen bazaio, bere karratua ematen du: x+1=x^2</li>
</ul>
Aurreko bi ekuazioetan, x ezezaguna Phi zenbakia da.<br />
borthuzai 2007-03-09 14:34 #4
:-) ja, ja, ja, baneoan ba ni hire matematikari sena izkutuan gorde behar ote huen!<br />
Amuitz 2007-03-09 16:59 #5
Nire irakasgaiaren orrian (matematika ordenadorez) lotura egin zioat post honi, ea orain nire ikasleak agertzen hasten zaizkian!<br /><em>(ez diat uste gehiegi emozionatzen direnik gauza hauekin, ordea)</em><br />
Utzi iruzkina: